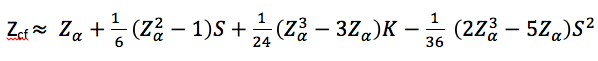Många av mina kunder använder sig av olika riskverktyg såsom stress test, scenario analys och VAR för att analysera riskerna med hedgefonder.

Jag får ofta frågor av mina kunder vad är ”Modified VAR (MVAR)”?  Skall vi använda MVAR istället för VAR, när det kommer till hedgefonder? Kan två fonder med samma VAR ha olika MVAR? MVAR verkar både komplicerat och svårt att praktiskt implementera?

I denna artikel tänkte jag försöka sticka håll på myten att MVAR är både komplicerad och svår att implementera. Man behöver inte vara något matematiskt geni eller ha tillgång till avancerade interna risksystem för att kunna hantera MVAR. Med lite grundläggande matematik och VBA programmeringskunskaper kan man enkelt implementera MVAR i Excel.

Både VAR och MVAR modeller har sina brister och har kritiserats av både akademiker och marknadspraktiker för att bland annat, invagga investerare i en falsk risksäkerhet, leda till ett extremt risktagande utanför svansarna, man fokusera på risk man kan hantera och tar egentligen inte hänsyn till risken utanför svansarna osv.  Även om dessa diskussioner är intressanta och relevanta, så kommer jag i denna artikel att fokusera på skillnaden mellan VAR och MVAR.

Den traditionella VAR modellen förutsätter att fondens avkastning är normalfördelad över den givna tidsperioden. Fördelning av fondens avkastning kan beskrivas av de två statistiska parametrarna µ (medelvärde) och σ (standardavvikelse). (För en normalfördelad kurva är µ=0 and σ=1.) För att skatta populationsparametrar för given konfidensgrad används det kritiska värdet Z_α för det givna konfidensintervallet. (Vanligaste konfidensintervallet är 95 %, med kritiskt värde  och  99 % med ett kritiskt värde )  VAR för fondens historiska avkastning är en funktion av konfidensintervallet Z_α multiplicerat med standardavvikelsen(ơ). (För en normalfördelad kurva är µ=0).

VAR_(1-α) = µ-Z_ασ

Hedgefonders avkastning är vanligtvis inte normalfördelade och har en mer asymmetrisk avkastningsfördelning, generellt sett fetare svansar, en mer negativ/positiv skevhet och en mer övervägande negativ/positiv kurtosis i jämförelse med traditionella ”long-only” fonder. Det kan också finnas stora skillnader mellan enskilda hedgefonder som uppvisar en liknande VAR fördelning.

Vad skiljer då MVAR från den traditionella VAR, och vad gör den lämpligare att använda, när det kommer till hedgefonder. MVAR beaktar den tredje (M3) och fjärde (M4) ordningen av avkastningsfördelningen det vill säga skevheten och kurtosis (d.v.s. tredje och fjärde derivatan).  För att lösa problemet med skevheten och kurtosis måste den traditionella VAR-formeln utökas och inkludera den välkända Cornish-Fisher expansionen.

Z_cf är det kritiska värdet av Cornish-Fisher vid respektive konfidensintervall, S är urvalsskevheten och K är urvalskurtosisen. Skulle avkastningskurvan var normalfördelad kommer S och K att vara lika med noll och vi kan därför skriva,

Z_cf = Z_α

Låt oss nu definiera funktion MVAR:

MVAR_1-α =µ -Z_cfơ

Den givna fondförlusten kommer nu istället att vara en funktion av det givna kritiska värdet av Cornish-Fisher multiplicerat med standardavvikelsen, till skillnad från konfidensintervallet i den traditionella VAR-modellen.

Efter att vi nu har definierat den matematiska terminologin bakom MVAR låt oss nu med lite enkel VBA programmering se, hur vi kan implementera MVAR i Excel.  För enkelhetens skull kommer jag skriva förklaringarna på subrutinerna på svenska, och jag har redan förprogrammerat funktionerna; medelvärde (mean), standardavvikelse (std), skevhet(skewness) och kurtosis(kurt), vilka torde var bekanta för det flesta läsarna. Det finns annars åtskilliga böcker och internet sidor om, hur man programmerar dessa funktioner.

Excel VBA-kod för MVAR 

Jag hoppas, att jag hjälpt till, att sticka håll på myten om MVAR och visat hur lätt man kan implementera MVAR i Excel.

Bild: (c) everything-possible—shutterstock.com